
| Experiments Menu | Main Menu | Next Page |
|---|

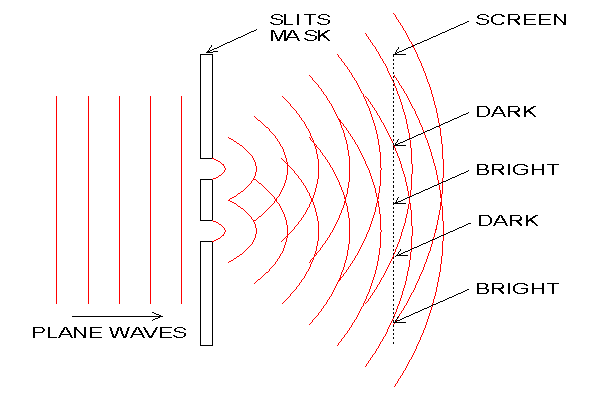
The above graphic shows the basic Young's slits experiment. Considering the light as a wave, it is not difficult to see how interference occurs. Each slit acts like a new source of waves. The waves spread out (diffract) from each slit and begin to overlap. Like water waves, where a wave crest from one source coincides with a crest from the other source, they reinforce each other. The amplitude of the wave at that point is then doubled. Where a crest coincides with a trough, they cancel each other out resulting in zero amplitude (flat) at that point. Because the waves emanating from the two slits were originally from the same source, they always keep in step with each other. At the screen this results in bands of light where reinforcement is occurring and dark where cancellation is occurring. These bands or 'fringes' are called a diffraction pattern. The distance between the fringes y = λD/a where λ (pronounced lambda) is the wavelength of the light, D is the distance from the slits to the screen and 'a' is the distance between the slits. All lengths must be in the same units (usually meters).
To produce fringes that are visible to the unaided eye, the distance between the slits needs to be very small. For example, consider green light with a wavelength of 520nm (0.000,000,52 meters). If the fringes are to be 1mm apart and the distance from the slit mask to the screen is 1m, then a = λD/y = (520x10-9 x 1) / 0.001 = 520x10-6. This means that the slits would need to be 0.52mm apart.
The way in which information about an object is transferred by light (or any electromagnetic wave) is rather interesting. The diffraction pattern of an aperture mask (or any object) is not just a meaningless pattern. It contains a description of the object. Proof of this is that an ordinary lens can be used to convert the diffraction pattern back into an image of the object. This is how the human eye works. The light arriving at your eyes is a diffraction pattern of the objects that you are looking at. Your eyes convert the diffraction pattern back into an image on the retina.
It is not normally possible to see how information describing an object is encoded in the diffraction pattern. The reason for this is that most objects have a complicated shape and light is normally composed of a range of wavelengths. To see what is happening it is necessary to simplify things. The simplest light source in this context is a coherent monochromatic (single wavelength) source such as a laser. The simplest object is a sinusoidal diffraction grating.
A sinusoidal diffraction grating is like a very fine venetian blind. However, rather than alternating abruptly between clear and opaque, the light transmission of a sinusoidal grating varies smoothly in a sinusoidal profile. When a monochromatic light beam is passed through a sinusoidal grating, it is split into three beams. One beam goes straight through and the other two are at equal angles to the straight through beam.

In the photograph above, a 405nm laser beam is passing through a tank of water dosed with fluorescein dye. The laser light has a short enough wavelength to make the dye fluoresce. The laser is on the left, outside the tank. In the left hand end of the tank, immersed in the water, is a sinusoidal diffraction grating. The grating has 1000 lines per mm. The 'straight through' beam and the two symmetrical side beams can be clearly seen. The laser, the dye and the diffraction grating were obtained on eBay.
The number of lines per mm of the grating is called the frequency of the grating, or more specifically the spacial frequency. If the frequency of the grating were increased, the angle between the beams would increase in proportion (for small angles). In other words, the angle between the beams is proportional to the spacial frequency of the grating. The relationship is d Sin θ = λ where d is the period of the grating , θ is the angle of the beam from the normal and λ is the wavelength of the light.
If the diffraction grating had more spacial frequency components, a pair of beams would be generated for each of them. This ability to split a pattern into its individual sinusoidal components is called a Fourier transform. A diffraction pattern is therefore the optical Fourier transform of the object.
Knowing that the diffraction pattern is the optical Fourier transform of the object might give you a clue as to what the 'straight through' beam represents. This beam corresponds to the zero spacial frequency component of the grating.
There are more diffraction patterns and further explanation on the Diffraction page.
For small divergence angles, the angle is proportional to the wavelength of the light. This can be seen by transposing the above formula to θ = Sin-1(λ / d). Therefore, if an object is illuminated with white light, there will be a different sized diffraction pattern for each wavelength, all superimposed on each other.
Although light travels like a wave, it is always emitted and detected as particle-like quanta known as photons. It is tempting to think of light quanta as just short bursts of wave. However, electrons, protons, neutrons and even whole atoms and molecules can behave as waves. All such entities exhibit wave / particle duality.
The particle nature of light is revealed in the photoelectric effect. The photoelectric effect is the phenomenon whereby light shining on a metal surface causes electrons to be emitted from that surface. If light were simply a wave, the energy in the wave would be shared equally between all the electrons on the metal surface. It would then be expected that the energy of the emitted electrons would be proportional to the intensity of the light and as the intensity was reduced, at some point there would be insufficient energy and no electrons would be emitted. However this is not the case. In practice, for any particular wavelength of light, all the electrons emitted have the same energy, regardless of the intensity of the light. As the intensity of the light is reduced, there is no cut-off, the rate of emission of electrons simply reduces. Furthermore, the energy of the emitted electrons is proportional to the frequency of the light.
Albert Einstein explained this by saying that the light is composed of particles, each with energy E = hf where h is Planck's constant (6.626x10-34Js) and f is the frequency of the light in Hz. In words, the energy of a photon is proportional to the wave frequency of the light. This is touched upon on the X-Rays page.
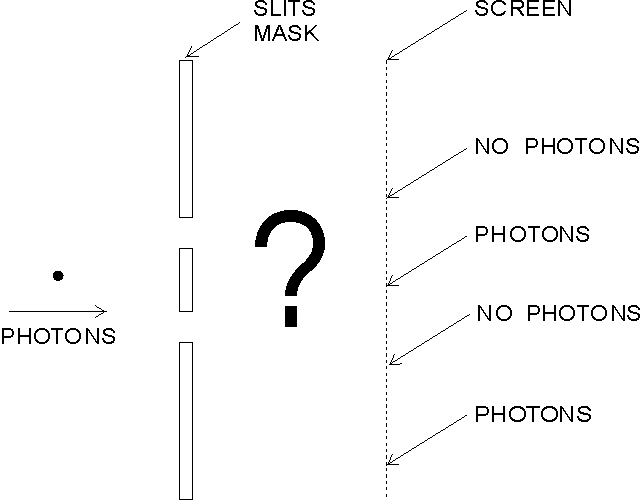
The above graphic shows the basic Young's slits experiment again. This time, the intensity of the light source is greatly reduced to the point where only one photon passes through the apparatus at a time. If a sensitive detector is now placed at each slit, each photon will be detected at one slit or the other, never both. This seems to indicate that light is made of particles and each particle goes through one slit, as common sense would suggest.
If the screen is replaced by a very sensitive video camera, little flashes will be registered on the monitor screen. Each of these flashes indicates the detection of a photon. If the monitor is a storage device, so that each registered flash is displayed continuously (integrated) then dots will gradually build up on the screen. At first their positions look random, but after a period of time the familiar bands of the interference pattern appear. For this to happen, each photon must have somehow been influenced by both slits. Any attempt to detect without doubt, which slit each photon went through, results in the interference pattern failing to appear. The interference pattern is identical regardless of the rate of the photons, which implies that interference between photons does not happen.
In quantum physics this is explained by Heisenberg's uncertainty principle.
In its modern form it is stated as
σxσp ≥ h/4π where
σx (pronounced sigma X) is the standard deviation
(uncertainty) of position, σp is the standard
deviation of momentum and h is Planck's constant. What this means is that the
position and momentum of a particle are never both fully defined. If a particle's
position is measured accurately, its momentum becomes uncertain and vice versa.
In the absence of measurement, each photon is able to spread out as a wave passing through both slits. The square of the amplitude of this wave at any point represents the probability that a photon would be detected at that location. At the camera, the photon is detected and its position then becomes certain. Where on the screen each photon will appear can not be known in advance, it is completely probabilistic. It seems that reality, at least as we know it, does not exist at the sub-atomic scale.
In a way, each slit acts like a measurement device, in that for a photon to pass on to the screen or camera, it must pass through one of those small areas. It's location is therefore restricted at the point in time when it passes through the slits. This makes its momentum uncertain. Being a vector property, uncertain momentum causes the photon to spread out (diffract) from each slit. Each slit only restricts the photon in the horizontal direction, so it only spreads out in the horizontal plane.
It was once thought that the universe consisted solely of billiard ball like particles and that if it were possible to know the position and momentum of every particle in the Universe it would be possible to completely predict the past and the future. However, not only is knowing the position and momentum of every particle in the Universe not practical, but due to the uncertainty principle, knowing the position and momentum of just a single particle is impossible.
It is useful to have some appreciation of the magnitude of a single photon. The formula E=hf gives the energy of a single photon as described above. The frequency f is related to the wavelength λ by the relationship c=fλ where c is the speed of light (3x108ms-1). The mid-point of the visible spectrum is around 550nm, which is a green/yellow colour. The frequency f=c/λ = 3x108 / 550x10-9 = 545x1012Hz. The energy E=hf = 6.626x10-34 x 545x1012 = 3.6x10-19J.
One watt is a joule per second. This means that if you have a lamp producing 1W of light, it is emitting around 1 / 3.6x10-19 = 2.8x1018 photons per second. At the time of writing, my electricity was costing about 15p/kWh (1.4x10-8£/J). This means that a visible photon is worth about £1.5x10-26. This is why they are still free.
The next page shows the parallels between optical diffraction and electrical waveforms.
| Page Title | Description |
|---|---|
| Information Encoding | This page attempts to show the similarities between the frequency content of an electrical waveform and the diffraction pattern of an object. |
| Project Construction | Information about how the experiment was built. |
| Single Photon Justification | Mathematical justification that the experiment can be considered to be diffracting individual photons. |
| Quiz | A multiple choice quiz (requires Java). |
| Instructions | Instructions for operation of the experiment. |
| Online Experiment | The live interactive Young's slits experiment. Please read the instructions first. |
| Conclusion | Conclusion and references. |
| Experiments Menu | Main Menu | Next Page |
|---|